Proportionnalité et
fonction linéaire
Pourquoi est-ce si difficile d’enseigner la proportionnalité ? Pourquoi passe-t-on autant de temps à faire comprendre cette première modélisation mathématique qui nous paraît si simple ? Marie-Jeanne Perrin-Glorian et Daniel Perrin nous livrent ici quelques éléments de réponse à ces questions.
Daniel Perrin et Marie-Jeanne Perrin-Glorian
© APMEP Juin 2021
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Introduction
Écrire un article sur la proportionnalité pour la revue de l’APMEP est une gageure. En effet, sur ce sujet, on peut considérer que tout a été dit, vu le nombre d’ouvrages, d’articles parus dans des revues comme Petit \(x\) ou Repères-IREM, dans les brochures des IREM et les documents d’accompagnement des programmes de l’école ou du collège. D’ailleurs, beaucoup des choses que nous allons dire sont déjà dans le texte de la COPREM1 publié en 1986, injustement oublié aujourd’hui. Nous avons cependant accepté de relever le défi de présenter, dans un format court, une synthèse des points qui nous paraissent fondamentaux, renvoyant le lecteur aux références pour plus de précisions.
1. Deux points de vue sur la proportionnalité
Il nous paraît important de distinguer dès le début de cet article deux points de vue sur la proportionnalité, à la fois pour considérer l’apprentissage de cette notion sur toute la scolarité obligatoire et parce que le point de vue optimal dépend des situations. Prenons un premier exemple très simple pour éclairer la définition de la proportionnalité selon ces deux points de vue.
| Premier exemple |
|---|
| Un pot de crème fraîche de 20 cl pèse 196 g. Combien pèse un pot de 50 cl ? Un pot de 125 cl ? |
Une relation entre deux grandeurs
Le premier point de vue, historiquement le plus ancien, est celui d’une relation entre deux suites de grandeurs2, vérifiant des propriétés d’additivité et de conservation des rapports scalaires entre les grandeurs d’une même suite.
Sur notre exemple, on peut dire qu’un pot de 40 cl pèse deux fois plus, soit 392 g, qu’un pot de 10 cl pèse deux fois moins soit 98 g et qu’un pot de 50 cl pèse 392 g + 98 g soit 490 g puisque (ou \(5 \times 98\) g puisque (50 cl =5\( \times 10\) cl). On peut dire ensuite que 25 cl pèsent 245 g et 100 cl pèsent 980 g et donc 125 cl pèsent 1225 g.
Ainsi, dans le Monge et Guinchan de Troisième (1959), on trouve la définition suivante (en termes modernes on reconnaît un homomorphisme3) :
On dit que deux grandeurs mesurables sont proportionnelles si, lorsqu’on multiplie (ou l’on divise) la mesure de l’une par \({2}\), \({3}\), \({4}\), …, la mesure correspondante de l’autre est multipliée ( ou divisée ) par \({2}\), \({3}\), \({4}\), …
C’est essentiellement le point de vue d’Euclide dont la théorie des grandeurs et proportions a prévalu pendant des siècles pour justifier la proportionnalité avant que ne soit élucidée la notion de fonction. Euclide ne considère que des rapports de grandeurs de même espèce et, pour lui, ces rapports ne sont pas des nombres (seuls les entiers ont statut de nombre). Ainsi, il n’écrit jamais4 : posons \(\lambda=\dfrac{\mathstrut a}{\mathstrut b}\), ce qui le conduit à des formulations alambiquées :
On dit de quatre grandeurs \(a\), \(b\), \(c\) et \(d\), prises dans cet ordre, que la première est à la deuxième dans le même rapport que la troisième est à la quatrième, quand n’importe quel équimultiple de la première et de la troisième grandeur est en même temps et respectivement soit supérieur, soit égal, soit inférieur à n’importe quel (autre) équimultiple de la deuxième et de la quatrième grandeur.
En langage moderne, cela peut se traduire par :
Les rapports \(\dfrac{\mathstrut a}{\mathstrut b}\) et \(\dfrac{\mathstrut c}{\mathstrut d}\) sont égaux si pour tous \(q\), \(p\) appartenant à \(\mathbb{N}\), on a \(qa> pb\) si et seulement si \(qc> pd\) ; \(qa=pb\) si et seulement si \(qc=pd\) et \(qa< pb\) si et seulement si \(qc< pd\).
Nous n’en dirons pas plus sur ce sujet.
Une fonction linéaire
Une autre manière de traiter notre exemple (surtout si l’on veut trouver la masse de crème pour n’importe quel volume) est de rechercher la masse volumique de la crème fraîche en divisant \(196\) par \(20\). La masse volumique est de 9,8 g/cl ou 98 g/dl ou 980 g/l. Si l’on a un volume de crème mesuré en cl, on multiplie cette mesure par la masse volumique en g/cl et on obtient la mesure de la masse en g. Ici 9,8 g/cl \( \times 50 cl=490\) g et 9,8 g/cl \(\times 125\) g=1225 g. C’est le point de vue fonctionnel que l’on peut définir ainsi :
| On a une relation de proportionnalité entre l’ensemble \(A\) de grandeurs mesurées avec l’unité \(u\) et l’ensemble \(B\) de grandeurs mesurées avec l’unité \(v\), s’il existe une fonction réelle linéaire qui relie les mesures des grandeurs de \(A\) et \(B\), c’est-à-dire un nombre réel \(a\) tel que \(y=ax\) où \(x\) est une mesure de \(A\) avec l’unité \(u\) et \(y\) est une mesure de \(B\) avec l’unité \(v\). |
Le nombre \(a\) est lui-même la mesure d’une autre grandeur dans une unité définie à partir de \(u\) et \(v\). Nous y reviendrons.
Dans le cas de suites proportionnelles de nombres \((x_i)\) et \((y_i)\), le point de vue fonctionnel consiste à dire qu’il existe un nombre \(a\) tel que, pour tout \(i\), \(y_i=ax_i\) ; le point de vue homomorphisme dit que, pour tous \(i\), \(j\), \(k\), si \(x_k=x_i+x_j\), alors \(y_k=y_i+y_j\) et que, pour tout \(\lambda\), pour tous \(i\), \(j\), si \(x_j=\lambda x_i\), alors \(y_j=\lambda y_i\). En particulier, on peut étendre des suites proportionnelles en ajoutant les couples somme ou produit par un scalaire s’ils n’y étaient pas : on a encore des suites proportionnelles. La proportionnalité entre suites de nombres peut aussi s’exprimer par l’égalité des rapports \(\dfrac{\mathstrut x_i}{\mathstrut y_i}\cdotp\)
En particulier, si les rapports \(\dfrac{\mathstrut x_i}{\mathstrut y_i}\) et \(\dfrac{\mathstrut x_j}{\mathstrut y_j}\) sont égaux, il en est de même de \(\dfrac{\mathstrut x_i+x_j}{\mathstrut y_i+y_j}\) et \(\dfrac{\mathstrut x_i-x_j}{\mathstrut y_i-y_j}\cdotp\)
La preuve est évidente et découle de la distributivité de la multiplication par rapport à l’addition si, contrairement à Euclide, on donne un nom au rapport : \(\dfrac{\mathstrut x_i}{\mathstrut y_i}=k\). On peut alors écrire \(x_i=ky_i\), \(x_j=ky_j\) donc \(x_i+x_j=ky_i+ky_j=k(y_i+y_j)\) etc.
Nous reviendrons à plusieurs reprises sur ces deux points de vue mais montrons déjà par deux exemples l’intérêt de chacun d’eux dans des situations plus complexes.
Exemple des pourcentages d’augmentation et de réduction
Le point de vue fonction est indispensable si l’on veut de plus opérer sur les fonctions linéaires en jeu, par exemple les ajouter ou les retrancher, comme c’est le cas dans les pourcentages d’augmentation et de réduction. Prenons l’exemple du calcul d’un prix TTC ou HT avec une TVA de 20 %. La TVA est proportionnelle au prix du produit hors taxe et cela entraîne que le prix TTC, \(P\), est lui aussi proportionnel au prix HT, \(p\). Pour calculer le prix TTC à partir du prix HT, la plupart des gens à qui se pose le problème calculent la taxe \(t={0,2}p\) puis l’ajoutent au prix HT5. C’est correct mais, si l’on n’a pas besoin de connaître la valeur de la taxe, on peut obtenir le résultat plus rapidement en considérant la relation de proportionnalité entre \(p\) et \(P\) : \(P={1,2}p\) (\(P=p+t=p+{0,2}p=(1+{0,2})p={1,2}p\)). En revanche, si l’on cherche le prix HT à partir du prix TTC, la considération de la fonction devient indispensable pour pouvoir l’inverser. Par exemple, pour une TVA de \(20\) %, nous avons vu que \(P={1,2}p\). On obtient donc \(p\) en divisant \(P\) par \({1,2}\) : \(p=\dfrac{\mathstrut P}{\mathstrut {1,2}}\cdotp\) L’ écriture de cette relation n’est possible que si l’on a identifié le coefficient de proportionnalité \({1,2}\). Pour obtenir la valeur de la taxe à partir du prix TTC, il faut voir que la taxe est elle aussi proportionnelle au prix TTC : \(t=P-p=P-\dfrac{\mathstrut P}{\mathstrut {1,2}}\) mais aussi \(t={0,2}p=\dfrac{\mathstrut {0,2}}{\mathstrut {1,2}}P\). On voit ici toute la force de l’algèbre qui permet de faire le calcul sous une forme générique et de calculer sur le prix hors taxe avant de le connaître.
Exemple des partages proportionnels
Ce type de question utilise fondamentalement le point de vue « homomorphisme » .
Voici sur le sujet un des exercices les plus simples du Monge et Guinchan de Troisième (1959)
| Deuxième exemple |
|---|
| Une somme a été partagée entre trois personnes de manière que les parts soient proportionnelles aux nombres \(2\), \(3\) et \(5\). La troisième personne a reçu \({2400}\) F de plus que la deuxième. Quelle était la somme à partager ? |
Ici intervient de façon essentielle la linéarité (voir § 3 ) : la différence entre deux parts est dans la même proportion que la différence des nombres auxquels ces parts sont proportionnelles. Appelons \(S\) la somme à partager et \(a\), \(b\) et \(c\) les trois parts. On a \(\dfrac{\mathstrut a}{\mathstrut 2}=\dfrac{\mathstrut b}{\mathstrut 3}=\dfrac{\mathstrut c}{\mathstrut 5}=\dfrac{\mathstrut c-b}{\mathstrut 5-3}=\dfrac{\mathstrut S}{\mathstrut 2+3+5}\cdotp\)
On conclut grâce à \(c-b={2400}\).
Soulignons que les exercices de ce type, classiques autrefois mais oubliés pendant de nombreuses années, reviennent dans les programmes de 20186 derrière le terme « ratio » :
On dit, par exemple,
- que deux nombres \(a\) et \(b\) sont dans le ratio \(2\,{ :}\,3\) (notation standardisée) si \(\dfrac{\mathstrut a}{\mathstrut 2}=\dfrac{\mathstrut b}{\mathstrut 3}\) ;
- que trois nombres \(a\), \(b\) et \(c\) sont dans le ratio \(2\,{ :}\,3\,{ :}\,7\) (notation standardisée) si \(\dfrac{\mathstrut a}{\mathstrut 2}=\dfrac{\mathstrut b}{\mathstrut 3}=\dfrac{\mathstrut c}{\mathstrut 7}\cdotp\) »
L’exercice qui suit, issu aussi du Monge et Guinchan (1959), est plus difficile car il faut à la fois considérer la somme dont on dispose réellement (somme des quantités obtenues soit \({3681}\) F) et la somme demandée soit \({4090}\) F :
| Troisième exemple |
|---|
| Une somme d’argent doit être partagée entre deux personnes. Le total de ce qu’elles demandent dépasse de \(409\) F le montant de la somme ; le partage étant fait proportionnellement à leurs demandes, la première personne reçoit \({2025}\) F et la deuxième \({1656}\) F. Combien chacune d’elles réclame-t-elle ? |
Si on appelle \(a\) et \(b\) les sommes demandées, on a donc \(\dfrac{\mathstrut a}{\mathstrut {2025}}=\dfrac{\mathstrut b}{\mathstrut {1656}}=\dfrac{\mathstrut a+b}{\mathstrut {2025}+{1656}}=\dfrac{\mathstrut {4090}}{\mathstrut {3681}}\cdotp\)
À l’époque il n’y avait pas de calculatrice mais le calcul s’arrange bien : le total demandé est égal à \({4090}\) (\(409\times 10\)) donc \({3681}\) est égal à \(9\times409\) et \({2025}\) et \({1656}\) sont des multiples de \(9\) !
2. Les grandeurs et la mesure des grandeurs
Nous apportons dans ce paragraphe quelques repères sur la notion de grandeur, en nous limitant à ce qui est indispensable pour parler de proportionnalité.
Ainsi nous ne considérerons que des grandeurs mesurables 7 avec une mesure positive.
| Une grandeur est associée à un objet matériel dont elle décrit un aspect. Ainsi on peut parler de la longueur d’un meuble, de l’aire qu’il occupe au sol, de son volume, de sa masse, de son prix, toutes ces caractéristiques étant des grandeurs de différentes natures (ou espèces : on parle traditionnellement de grandeurs de même espèce). |
Notons que le mot « grandeur » est utilisé dans plusieurs sens selon le contexte : par exemple, le mot longueur peut signifier l’espèce longueur, parmi les grandeurs, ou la longueur d’un objet particulier.
Lorsqu’on a choisi une unité, on peut mesurer les grandeurs. Les mesures des grandeurs sont des nombres réels et on obtient ainsi un « isomorphisme » entre grandeurs et nombres réels positifs . Bien entendu, changer d’unité change la mesure, mais pas la grandeur. Ainsi, on a 1 km = 1 000 m = 100 000 cm. Nous parlerons de grandeur mesurée quand la grandeur est désignée sous la forme d’un nombre suivi d’une unité. La notion de grandeur peut être définie à partir de celle de mesure : si l’on a une fonction mesure définie sur un ensemble d’objets et à valeurs dans \(\mathbb{R}^{+}\), une grandeur est une classe d’équivalence pour la relation « avoir même mesure » . Une espèce de grandeur est l’ensemble quotient pour cette fonction mesure. Pour certaines grandeurs, on a des instruments qui permettent de définir l’équivalence « avoir même grandeur » sans passer par la mesure, au moins dans un certain domaine, par exemple les masses avec une balance Roberval ou les longueurs de segments avec un compas mais ce n’est pas possible pour d’autres : par exemple le découpage et recollement permet de décider de l’égalité de l’aire dans certains cas mais pas de dire si un carré a même aire qu’un disque ou non.
On peut comparer des grandeurs de même espèce, les additionner, multiplier une grandeur par un nombre réel positif. En revanche, pour définir le produit de deux grandeurs, il faut avoir défini la grandeur produit (par exemple l’aire pour le produit de deux longueurs). En ce qui concerne les rapports, on peut faire en tous cas le rapport de deux grandeurs de même nature (le rapport \(\dfrac{\mathstrut y}{\mathstrut x}\) est alors le nombre \(a\) tel que \(y=ax\)). Cela permet de définir la proportionnalité par la constance du rapport entre les grandeurs qui se correspondent dans le cas où ces grandeurs sont de même espèce, par exemple les situations d’agrandissement ou de réduction comme les cartes et les plans. Encore faudrait-il distinguer, d’un point de vue didactique, le cas où les grandeurs sont ou non mesurées dans la même unité : par exemple une échelle peut être donnée sous la forme \(\dfrac{\mathstrut1}{\mathstrut{100000}}\) ou sous la forme 1 cm représente1 km Nous y reviendrons plus loin.
Cependant, dans la plupart des relations de proportionnalité, les grandeurs en jeu ne sont pas de même espèce, par exemple la distance parcourue et le temps. On peut contourner le problème en choisissant des unités pour chacune des grandeurs, et en se ramenant au rapport des mesures des grandeurs concernées. C’est le point de vue qui a prévalu dans l’enseignement entre 1969 et 1995 où les grandeurs avaient disparu de l’enseignement des mathématiques. On ne parlait alors de proportionnalité qu’entre suites de nombres qui pouvaient être des mesures de grandeurs, une fois l’unité fixée.
On peut aussi, dans le cas d’une relation de proportionnalité entre des ensembles de grandeurs \(A\) et \(B\), définir une grandeur quotient qui aura sa propre unité, dérivée des unités choisies pour les grandeurs \(A\) et \(B\). Le quotient a un sens mais c’est devenu une grandeur.
Par exemple avec les distances et les durées, le quotient \(\dfrac{\mathstrut d}{\mathstrut t}\) est une vitesse qui, si \(d\) est en km et \(t\) en heures, sera exprimée en km/h. Le quotient d’une tension par une intensité, \(R=\dfrac{\mathstrut U}{\mathstrut I}\) est une résistance, exprimée en ohms si \(U\) est en volts et \(I\) en ampères. Dans le cas familier des situations d’achat où le prix payé est proportionnel à la masse du produit acheté, la grandeur quotient est le prix par unité de masse, mesuré par exemple en € /kg.
La considération d’une grandeur quotient est essentielle pour comprendre les changements d’unité. Par exemple, lorsqu’un athlète court le 100 m en 10 secondes, sa vitesse est de 10 m/s, mais aussi de 36 km/h parce que 1 h = 3 600 s et 1 km = 1 000 m.
Les grandeurs sont revenues dans les programmes de 1995, notamment à propos des changements d’unités pour les vitesses (mentionnés explicitement dans le programme de cycle 4 pour les niveaux Cinquième et Quatrième) et de la proportionnalité, présente à tous les niveaux et reliée à la fonction linéaire en classe de Troisième. Elles restent cependant mal aimées et mal comprises des professeurs.
La référence aux grandeurs permet de raisonner en s’appuyant sur le sens que chacune des opérations effectuées prend dans la situation décrite par le problème. Cependant, il est nécessaire aussi de pouvoir s’affranchir du sens dans la situation pour raisonner algébriquement, en se servant des propriétés des opérations pour effectuer les calculs. Ainsi, une multiplication qui a le sens d’addition répétée n’est pas naturellement commutative. Prenons l’exemple d’un salarié, payé (congés payés inclus) à 15 € de l’heure, qui travaille 27 h par semaine sur 40 semaines pendant l’année. On peut calculer le salaire annuel de deux manières en s’appuyant sur le sens du problème :
- le salaire par semaine est de \(15\times 27\) € et donc pour l’année de \((15\times 27)\) € multiplié par \(40\) ;
- le nombre d’heures travaillées dans l’année est \(27\times 40\) et donc le salaire est 15 € multiplié par \((27\times40)\).
Les deux méthodes amènent à faire le produit des trois nombres \(15\), \(27\), \(40\) qu’on pourrait aussi bien effectuer en faisant \((15\times40)\times27\) en utilisant l’associativité et la commutativité de la multiplication. Ce dernier calcul est le plus commode à effectuer mentalement \((600\times27=300\times54={16200})\) alors qu’il n’a pas de sens dans le problème. En effet \(15\), qui est un nombre d’euros par heure, ne peut être multiplié que par une mesure exprimée en heures et non en semaines ; \(27\) est un nombre d’heures par semaine qu’on ne peut multiplier que par un nombre de semaines.
3. Repères mathématiques
Le but de ce paragraphe est de comprendre ce qui est derrière la notion de proportionnalité pour l’employer de manière efficace. Nous avons vu plus haut deux manières de définir la proportionnalité. Retenons qu’il s’agit d’une relation fonctionnelle, qui, à toute grandeur \(x\) d’un ensemble \(A\) associe une grandeur \(y\) d’un ensemble \(B\) et telle que le rapport \(a =\dfrac{y}{x}\) est constant. Le coefficient \(a\) est alors, en général, une grandeur et cela demande d’avoir défini la grandeur quotient des espèces de grandeurs dont relèvent \(x\) et \(y\). On pourra aussi écrire \(y = ax\) en définissant en même temps le produit de l’espèce de grandeur dont relève \(a\) par celle dont relève \(x\).
On peut définir la proportionnalité en restant dans le cadre numérique en fixant des unités \(u\) et \(v\) dans lesquelles sont mesurées les grandeurs \(x\) et \(y\): \(x = \xi u\) et \(y = \eta v\). La proportionnalité peut alors s’exprimer par l’existence d’un nombre \(\alpha\) tel que, pour tous \(\xi\) et \(\eta \), \(\eta=\alpha\xi \). Le nombre \(\alpha \) est alors la mesure de la grandeur \(a \) dans l’unité \(v/u \).
Ainsi la proportionnalité peut se définir à partir d’une fonction linéaire de \( \mathbb{R} \) dans \( \mathbb{R} \) sur laquelle nous allons montrer deux résultats importants.
| Théorème 1 |
|---|
Soit \(f\) une fonction de \(\mathbb{R}\) dans \(\mathbb{R}\). Les propriétés suivantes sont équivalentes :
|
On dit alors que \(f\) est une fonction linéaire. Le nombre \(a\) est appelé coefficient de proportionnalité.
Démonstration
Il est clair que Théorème1_3 implique Théorème1_2.
Montrons que Théorème1_2 implique Théorème1_1..
Pour \(x = 1\) et \(\lambda\) quelconque, Théorème1_2 nous donne \(f(\lambda) = \lambda f(1) = f(1)\lambda \) d’où la conclusion en renommant \(\lambda \) en \(x \) et en posant \(a = f(1) \).
Pour Théorème1_1 implique Théorème1_3, on utilise les propriétés des opérations dans \(\mathbb{R}\) : la distributivité de la multiplication par rapport à l’addition pour \(f(x + y) = a(x + y) = ax + ay = f(x)+f(y)\), l’associativité et la commutativité de la multiplication pour \(f(\lambda x) = a(\lambda x) = (a\lambda)x = (\lambda a)x = \lambda(ax) = \lambda f(x)\).
- Il y a deux cas particuliers: \(a = 0 \) où l’on trouve la fonction nulle et \(a = 1\) où l’on a l’identité;
- Peut-on alléger la condition Théorème1_3 ? Autrement dit, une fonction qui vérifie \(f(x+y) = f(x)+f(y)\) pour tous \(x\), \(y\) est-elle linéaire? On montre facilement qu’on a \(f(\lambda x) = \lambda f(x)\) pour tout \(\lambda\in\mathbb{Q}\), mais, pour conclure, il faut supposer par exemple que \(f\)est continue ou monotone;
- La formulation Théorème1_3 définit la fonction linéaire en dimension plus grande, mais alors la condition Théorème1_1 n’est vérifiée que dans le cas des homothéties. C’est pourquoi, nous parlerons de la propriété d’homothétie pour indiquer que nous utilisons la fonction \(x \longmapsto ax\) : c’est le deuxième point de vue identifié dans le premier paragraphe (fonction linéaire). Le premier point de vue (homomorphisme entre grandeurs) correspond à l’utilisation des propriétés \(f(x+y) = f(x)+f(y)\), que nous nommerons propriété d’additivité, et \(f(\lambda x) = \lambda f(x)\), que nous nommerons propriété d’homogénéité.
Contrairement à ce que l’on voit dans nombre de manuels, le fait que le graphe de la fonction linéaire soit une droite passant par l’origine est un théorème, dont la preuve repose essentiellement sur le théorème de Thalès :
| Théorème 2 |
|---|
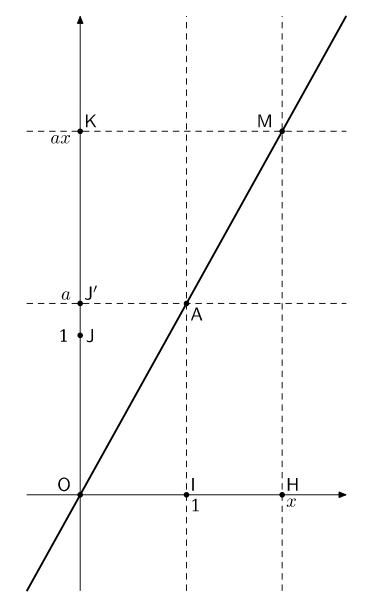
| Le graphe de l’application de \(\mathbb{R}\) dans \(\mathbb{R}\) définie par : \(x\longmapsto ax\) est une droite passant par \(\mathsf{O}\), origine du repère. |
Démonstration
On considère un repère orthogonal d’origine \( O\)
\(I\) et \(J\) sont respectivement les points d’abscisse \(1\) des axes \(x’\mathsf{O}x\) et \(y’\mathsf{O}y\).
\( A\) est le point de coordonnées \((1, a)\), \( J’\) est son projeté orthogonal sur l’axe des \( y\), et le point \( M\), d’abscisse \( x\), est situé sur la droite \((OA) \). On veut montrer qu’il a pour ordonnée \( ax\).
Soit \( H\) et \( K\) les projetés orthogonaux de \( M\) sur les axes. Alors, par Thalès, on a \(\dfrac{\overline{\mathsf{OH}}}{\overline{\mathsf{OI}}}=\dfrac{\overline{\mathsf{OM}}}{\overline{\mathsf{OA}}}=\dfrac{\overline{\mathsf{OK}}}{\overline{\mathsf{OJ’}}}\cdotp\) Comme \(\overline{\mathsf{OI}}=1\), \(\overline{\mathsf{OH}}=x\) et \(\overline{\mathsf{OJ}’}=a \), on en déduit \(\overline{\mathsf{OK}}= ax\).
Nous utilisons l’énoncé de Thalès avec mesures algébriques. Sinon, il faut considérer les positions.
Réciproquement, si \( N\) est le point de coordonnées \((x,ax)\), on introduit \( M\) d’abscisse \(x\) situé sur \((OA)\) comme ci-dessus. La démonstration précédente permet de dire qu’il est égal à \(N\) (mêmes coordonnées). Le point \(N\) est donc sur \((OA)\).
4. Éléments de réflexion didactique
Le but de ce paragraphe est d’identifier les différents types de problèmes liés à la proportionnalité, les différentes techniques de résolution, les représentations sémiotiques associées (graphes et tableaux) et les variables didactiques de ces problèmes.
Reconnaître une situation de proportionnalité
Les situations de proportionnalité relèvent de différents contextes. Cela peut être un contexte social, par exemple les achats, les salaires où l’on suppose un prix constant à l’unité, un salaire horaire ou mensuel fixé, ou encore les recettes de cuisine ou les pourcentages. Suivant la familiarité des élèves avec le contexte, la proportionnalité est alors plus ou moins facilement reconnue à travers des mots clés, des formulations standardisées [5]. Cela peut être un contexte physique, par exemple allongement d’un ressort, vitesse, masse volumique, débit. La reconnaissance de la proportionnalité est alors liée à la conceptualisation des grandeurs en jeu et peut être établie à partir d’un relevé de valeurs sur un graphique où l’on constate un alignement. Un excellent exemple est celui de la résistance d’un conducteur. La formule, pour un conducteur cylindrique de longueur \(l\) et de section \(s\), est \(R=\dfrac{\mathstrut\rho l}{\mathstrut s}\cdotp\) Elle dit simplement que \(R\) est proportionnel à \(l\) et inversement proportionnel à \(s\) et on donne un nom au « coefficient de proportionnalité » \(\rho\) (résistivité).
Cela peut être aussi un contexte géométrique comme les agrandissements et réductions.
Rappelons la situation bien connue d’agrandissement d’un puzzle proposée par Brousseau et décrite avec diverses variantes dans de nombreux textes .
Il s’agit d’agrandir un puzzle géométrique (dans le texte de Brousseau il s’agit du dessin d’un tangram, voir figure ci-dessous) en donnant la consigne sous la forme d’un couple (le côté qui mesure 4 cm sur le modèle doit mesurer 7 cm sur la figure agrandie).
| Les nombres ont été choisis de façon que le coefficient de proportionnalité ne soit pas évident et, quand on pose ce problème à des élèves de cycle 3 (CM ou Sixième), la plupart d’entre eux commencent par ajouter 3 cm à toutes les dimensions pour réaliser leur agrandissement. Si l’on choisit 8 cm au lieu de 7 cm, la plupart des élèves doubleront les dimensions mais rien n’assure alors qu’ils puissent reconnaître le modèle multiplicatif dans le cas général. |
Si l’on veut que les élèves apprennent quelque chose sur la proportionnalité à partir de cette situation, il est essentiel de réaliser aussi certaines conditions dans le choix du modèle à agrandir et dans l’organisation du travail des élèves. D’abord, il faut un partage du travail : chaque élève réalise une pièce et on procède à l’assemblage dans un deuxième temps, quand toutes les pièces sont réalisées ; c’est important pour éviter les les ajustements à l’œil.
Ensuite, au moment de l’assemblage, il faut que les élèves aient des raisons de rejeter le modèle erroné de l’addition. Ce sera le cas si le contour du puzzle reconstitué est un rectangle et si les côtés opposés de ce rectangle ne sont pas partagés en le même nombre de pièces, comme pour la reproduction du tangram. Le fait que le puzzle ne s’assemble pas correctement montre aux élèves qu’ajouter 3 cm à chaque ne convient pas.
Comment peuvent-ils faire évoluer leur procédure ? On peut les amener à formuler que 4 cm dans le modèle doit toujours donner 7 cm dans l’agrandissement. Alors, si l’on a quelque part 8 cm, cela doit donner 14 cm dans l’agrandissement ; si l’on a 6 cm, on peut le décomposer en 4 cm et 2 cm et chercher la valeur d’agrandissement de 2 cm ; 5 cm peut se décomposer en 4 cm et 1 cm. Ce sont les nécessités de la situation et l’appui sur l’additivité qui amènent à comprendre que la connaissance de l’agrandissement de 1 cm permet de connaître l’agrandissement de toutes les valeurs entières.
Les problèmes de proportionnalité et les techniques de résolution
Regardons d’abord le cas des problèmes de quatrième proportionnelle : on a deux grandeurs proportionnelles, on connaît deux valeurs pour l’une d’elles, une seule pour l’autre et on cherche la quatrième valeur. Par exemple, 18 m de tissu coûtent 189 € , combien coûtent 13 m ? Ou encore : dix objets identiques coûtent 22 € , combien coûtent quinze de ces objets ? Ou enfin : pour des stylos vendus à l’unité, on a payé 2,44 € pour 4 stylos ; un autre jour, on a payé 8,54 € , combien a-t-on acheté de stylos ?
L’égalité des rapports permet d’écrire \(\dfrac{\mathstrut a}{\mathstrut b}=\dfrac{\mathstrut x}{\mathstrut d}\) ou \(\dfrac{\mathstrut a}{\mathstrut b}=\dfrac{\mathstrut c}{\mathstrut x}\cdotp\) Si l’on raisonne sur les nombres, cela revient à \(ad=bx\) ou \(ax=bc\). Comme l’on disait autrefois « le produit des extrêmes est égal au produit des moyens » ou plus récemment « on fait le produit en croix » , ce qui amène à faire une multiplication suivie d’une division. Notons qu’on peut considérer deux types de rapports : ceux entre les grandeurs de même nature ou ceux entre mesures de grandeurs différentes. Pour l’exemple du tissu, en notant \(x\) l’inconnue, on peut écrire \(\dfrac{\mathstrut13}{\mathstrut18}=\dfrac{\mathstrut x}{\mathstrut189}\) ou \(\dfrac{\mathstrut189}{\mathstrut18}=\dfrac{\mathstrut x}{\mathstrut13}\) où le rapport exprime alors une mesure en € /m.
Une autre technique classique, enseignée à l’école primaire jusqu’aux années 1960 et mentionnée à nouveau dans les programmes, est le passage par l’unité ou la règle de trois. On raisonne sur les grandeurs : « J’ai payé 189 € pour 18 m de tissu, pour 1 m, je paierais 18 fois moins, soit 189 divisé par 18 et pour 13 m, je paierai 13 fois plus, soit \(\dfrac{\mathstrut{189}\times{13}}{\mathstrut{18}}\) » et on effectue la multiplication avant la division pour minimiser les erreurs d’arrondi.
Notons que l’exemple des stylos ne se prête pas aussi facilement à ce raisonnement sans expliciter le prix à l’unité. Le prix de 4 stylos est 2,44 €, le prix de 1 stylo est 4 fois moins, soit \(\dfrac{\mathstrut{2,44}}{\mathstrut4}\) € ; pour savoir combien on a acheté de stylos pour 8,54 €, il faut diviser \({8,54}\) par le prix d’un stylo ; sans effectuer la division, il faut avoir une bonne maîtrise du calcul sur les fractions pour écrire \(\dfrac{\mathstrut {8,54}\times\mathstrut 4}{\mathstrut {2,44}}\cdotp\) Ici, on trouve un nombre entier de centimes pour le prix d’un stylo donc le passage par l’unité stylo peut se faire. Sinon, avec la règle de trois directe, il faudrait dire « pour 2,44 €, j’ai 4 stylos, pour 1 € , j’aurais 2,44 fois moins soit \(\dfrac{\mathstrut{4}}{\mathstrut{2,44}}\) et pour 8,54 €, j’ai 8,54 fois plus. » Mais le calcul intermédiaire n’a pas de sens dans la situation car pour 1 € , on n’a pas un nombre entier de stylos.
C’est une des critiques traditionnellement apportées à la règle de trois : on raisonne sur les grandeurs mais avec des calculs intermédiaires qui n’ont pas nécessairement de sens.
Les représentations sémiotiques associées à la proportionnalité
Outre les écritures algébriques et les calculs numériques, diverses représentations sémiotiques sont associées à la proportionnalité, notamment les graphiques et les tableaux. Ces représentations interviennent de manière essentielle dans la résolution des problèmes liés à la proportionnalité. Nous avons vu que la proportionnalité est modélisée par une fonction linéaire dont le graphe est une droite passant par l’origine.
Le graphe est un moyen de donner rapidement des solutions approchées à un problème de quatrième proportionnelle ou de contrôler une solution obtenue par le calcul. La mise en avant du produit en croix a popularisé le tableau à quatre cases qui indique plus facilement quelles valeurs multiplier et par laquelle diviser. Encore faut-il remplir et respecter les marges du tableau qui indiquent les grandeurs en jeu et les unités.
Par exemple, pour le problème du tissu et celui des stylos :
| Longueur en m | 18 | 13 |
| Prix en euros | 189 | \(x\) |
| Nombre de stylos | 4 | \(x\) |
| Prix payé en euros | 2,44 | 8,54 |
Cependant, il est très utile de pouvoir enrichir le tableau et il est essentiel que les élèves apprennent à le faire pour introduire des valeurs intermédiaires qui facilitent la résolution, notamment la valeur \(1\). On a alors en fait le tableau de valeurs d’une fonction. Par exemple, dans le cas des stylos :
| Nombre de stylos | 4 | \(x\) | 1 |
| Prix payé en euros | 2,44 | 8,54 | 0,61 |
Nous avons fait le choix ici d’un tableau horizontal. Dans ce cas, les rapports entre colonnes sont des rapports scalaires variables ; le rapport entre les deux éléments d’une même colonne est, lui, constant ; c’est le coefficient de proportionnalité et c’est la mesure d’une grandeur quotient des grandeurs initiales. Ce n’est un nombre sans dimension que si toutes les grandeurs sont de même nature et mesurées dans la même unité.
Traiter une situation de proportionnalité : les variables didactiques
De nombreuses variables didactiques régissent les problèmes de proportionnalité. Nous avons déjà évoqué les grandeurs en jeu et les unités qui permettent de les mesurer, plus ou moins disponibles pour les élèves. Intéressons-nous maintenant à quelques autres variables.
Le nombre de variables en jeu
Il nous faut distinguer plusieurs cas. Dans l’exemple du salarié évoqué plus haut, le salaire payé est proportionnel au nombre d’heures travaillées, lui-même proportionnel au nombre de semaines travaillées. Il s’agit d’une composition de fonctions. Le cas de la proportionnalité multiple où une grandeur dépend linéairement de plusieurs paramètres est plus complexe : par exemple, l’aire d’un rectangle est proportionnelle à chacune de ses dimensions quand l’autre est fixée. Autre exemple : pour prévoir les achats pour l’accueil d’une collectivité, la quantité de pommes de terre à acheter est proportionnelle à la fois au nombre de personnes et à la durée du séjour. Dans la double proportionnalité, il peut être commode d’introduire un tableau à double entrée, pour traiter successivement les deux proportionnalités, notamment par un calcul mental. Par exemple dans le problème suivant : On prévoit d’acheter 3 kg de pommes de terre pour un séjour de \({5}\) personnes pendant \({6}\) jours. Combien faut-il prévoir pour un séjour de \({8}\) personnes pendant \({18}\) jours ? De \({15}\) personnes pendant \({10}\) jours ?
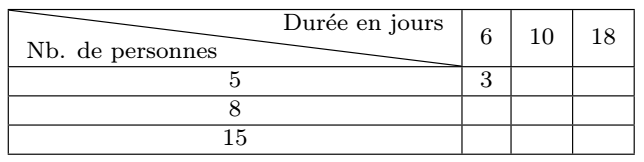
On peut passer de \(6\) jours à \(18\) jours pour \(5\) personnes sur la première ligne en multipliant par 9 kg puis de \(5\) personnes à \(8\) personnes dans la troisième colonne en multipliant par \(\dfrac{\mathstrut8}{\mathstrut5}\) (14,4 kg). Pour le deuxième, on peut passer de \(5\) personnes à \(15\) personnes dans la première colonne (9 kg) puis de \(6\) jours à \(10\) jours sur la troisième ligne en multipliant par \(\dfrac{\mathstrut10}{\mathstrut6}\) ou \(\dfrac{\mathstrut5}{\mathstrut3}\) (15 kg), en choisissant le chemin qui facilite les calculs.
Dans une évaluation ministérielle de 1980, publiée dans Études et documents 82-2, et citée dans le document de la COPREM [6], on demandait à des élèves de Sixième de compléter en \(5\) minutes les tableaux suivants à partir de l’information « En cinq minutes, une machine d’imprimerie effectue le tirage de \({50}\) journaux » :
| Minutes | Nombre de machines | Nombre de journaux |
|---|---|---|
| 5 | 1 | 50 |
| 5 | 3 |
| Minutes | Nombre de machines | Nombre de journaux |
|---|---|---|
| 5 | 1 | 50 |
| 5 | 50 |
| Minutes | Nombre de machines | Nombre de journaux |
|---|---|---|
| 5 | 1 | 50 |
| 2 | 500 |
La première question est réussie par la presque totalité des élèves alors que la dernière l’est par moins de 25 % des élèves. La disposition dans un tableau à double entrée entraînerait peut-être moins de différences entre les questions : il s’agit de remplir les cases où il y a un ? Pour la deuxième question, on peut raisonner en passant par les cases marquées \(\times\) et pour la troisième par les cases marquées \(\circ\).
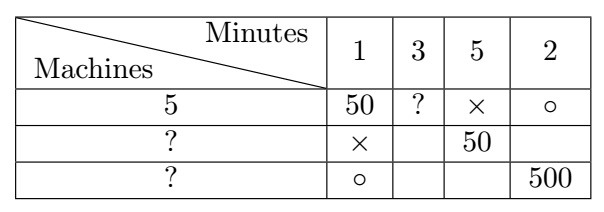
Remarquons cependant que la principale difficulté est sans doute que, dans les deux dernières questions, il faut trouver un antécédent (nombre de minutes) au lieu d’une image (nombre de journaux). C’est la même difficulté que dans le problème des stylos présenté plus haut.
Les problèmes où intervient une proportionnalité multiple se traduisent algébriquement par une fonction de plusieurs variables, du premier degré en chaque variable. Dans l’exemple des pommes de terre, si \(m\) est la masse de pommes de terres en kg, \(p\) le nombre de personnes et \(j\) le nombre de jours, il existe une constante \(k\) telle que \(m=kpj\). Cette constante représente la masse moyenne de pommes de terre consommées par une personne en un jour. On peut la déterminer à partir des données \(3=k\times5\times6\) donc \(k={0,1}\). Si l’utilisation de techniques comme les tableaux à double entrée revêt une importance au niveau du collège, notamment par rapport au calcul mental, il faut garder en tête que l’utilisation d’une formule comme \(m=kpj\), soit pour calculer \(m\) en connaissant \(p\) et \(j\), soit au contraire pour déterminer \(p\) ou \(j\) à partir des autres données, est un objectif essentiel en fin de collège et au lycée, dans la perspective des applications des mathématiques, en physique ou ailleurs.
Dans les recettes de cuisine, on a aussi en général plusieurs grandeurs en jeu mais il ne s’agit ni d’une composition de fonctions, ni d’une proportionnalité multiple : la variable est en fait un vecteur et le coefficient de proportionnalité est un scalaire : les quantités des différents ingrédients sont proportionnelles au nombre de personnes.
| Quatrième exemple | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pour faire un clafoutis aux cerises : pour \({4}\) personnes, il faut 500 g de cerises, \({3}\) œufs, 35 g de beurre, 30 cl de lait, 150 g de farine, 200 g de sucre. Quelles quantités faut-il prévoir pour 10 personnes ? On peut rassembler les informations dans un tableau
On traite autant de relations de proportionnalité que d’ingrédients, on peut aussi passer par un intermédiaire commode, ici deux personnes, et éventuellement remarquer de plus que \(10=8+2\) ou utiliser le rapport \({2,5}\) car \(10={2,5}\times4\). Évidemment se pose le problème des œufs pour lesquels il faudra à la fin choisir un peu plus ou un peu moins. |
Les nombres en jeu
Les nombres en jeu constituent aussi une variable didactique importante pour la reconnaissance et le traitement des problèmes de proportionnalité. Nous avons vu dans l’exemple des recettes qu’il pouvait être commode de passer par un intermédiaire. Prenons un autre exemple pour montrer que, dans un même problème, il peut être économique d’utiliser des techniques différentes selon les questions en tenant compte des valeurs numériques.
| Cinquième exemple | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
On se propose de peindre plusieurs pièces et le volume de peinture à utiliser est proportionnel à l’aire de la surface à peindre. On veut remplir le tableau suivant :
|
Ici plusieurs calculs sont à faire. On peut expliciter les coefficients de proportionnalité. Si on nomme \(A\) l’aire en \(m^2\) et \(V\) le volume en \(L\), on trouve facilement que \(A=14V\) (la colonne \((14,1)\) peut même être ajoutée au tableau) et donc \(V=\dfrac{\mathstrut A}{\mathstrut 14}\cdotp\) Cependant, on peut aussi se servir de valeurs connues pour en trouver d’autres et utiliser la linéarité pour plusieurs d’entre elles. Cette utilisation de la linéarité pour des valeurs particulières est utile pour le calcul mental. Elle est utile aussi pour l’apprentissage car elle donne aux élèves des points de repère et des moyens de contrôler leurs calculs. Ils peuvent aussi commencer par les valeurs faciles (\(a\), \(c\), \(e\)) et réfléchir pour les autres valeurs, ce qui peut les amener à rechercher le coefficient de proportionnalité dans un deuxième temps si cette technique n’était pas disponible d’emblée.
Pour trouver \(a\), on peut utiliser la relation entre \(7\) et \(35\) : \(35=5\times7\) donc \(a=5\times{0,5}={2,5}\) (propriété d’homogénéité). Pour \(c\), on peut remarquer que \({0,25}=\dfrac{\mathstrut {0,5}}{\mathstrut 2}\) d’où \({2,25}=2+{0,25}={0,5}\times4+{0,5}\times{0,5}={0,5}\times{4,5}\) et donc on trouve \(c=7\times{4,5}\) (additivité et homogénéité) (ou \(c=28+{3,5}\)). Pour \(e\), on peut utiliser la relation \({0,75}={0,5}\times{1,5}\) (homogénéité) ou \({0,75}={0,5}+{0,25}\) (additivité) donc \(e=7\times{1,5}={10,5}\) . On peut enrichir le tableau des valeurs trouvées.
On peut ensuite remarquer que \(41=35+6\) et \(6=3\times2\) ou \(6=7-1\). Cela peut encourager à chercher la valeur de \(b\) : en effet, on pourra trouver \(d\) en se servant de cette relation et des valeurs de \(a\) et \(b\). Mais, pour trouver \(b\), le plus simple est de chercher le coefficient de proportionnalité : pour \(1 m^2\), il faut \(\dfrac{\mathstrut {0,5}}{\mathstrut 7}\) l de peinture, donc pour \(2 m^2\), il faut \(\dfrac{\mathstrut 1}{\mathstrut 7}\) l (homothétie). Pour \(41 m^2 \), il en faut donc \({2,5}+3\times\dfrac{\mathstrut 1}{\mathstrut 7}\text{ l}={2,5}+\dfrac{\mathstrut 3}{\mathstrut 7}\) l (\(={2,93}\) à \(10^{-2}\) près). Pour \(f\), on peut utiliser \(50=49+1\) donc \(f=7\times{0,5}+\dfrac{\mathstrut{0,5}}{\mathstrut7}=3+\dfrac{\mathstrut 4}{\mathstrut 7}\) (additivité et homogénéité) ou directement
\(f=50\times\dfrac{\mathstrut {0,5}}{\mathstrut 7}=\dfrac{\mathstrut 25}{\mathstrut 7}=3+\dfrac{\mathstrut4}{\mathstrut7}\) (homothétie).
Pour \(g\), il faut chercher le coefficient de proportionnalité dans l’autre sens, soit l’aire que l’on peut peindre avec \(1\) litre de peinture, soit \(14 m^2\) . Donc \(g={1,3}\times14={18,2}\) (homothétie).
en particulier les représentations sémiotiques fournies ou non, constituent aussi une variable didactique des problèmes.
5. Des repères pour l’enseignement pour une progression du cycle 2 au lycée
Les situations de proportionnalité relèvent de contextes variés, mettent en jeu des grandeurs très diverses et interviennent de façon essentielle dans la construction du sens de la multiplication et de la division et c’est à tous les niveaux, du CE1 à la Troisième, que vont se développer les techniques de résolution des problèmes de proportionnalité, en interaction avec la construction des différentes grandeurs, des nombres et de leurs opérations et aussi le développement des connaissances algébriques8.
Dans les premières années (CE1, CE2), il s’agira essentiellement de situations de multiplication et de division dans le domaine des nombres entiers. Au cours moyen, en interaction avec l’introduction des fractions et des nombres décimaux et avec la mesure des grandeurs, on commence à aborder des problèmes de quatrième proportionnelle dans des contextes variés. L’étude se poursuit au long du cycle 3 qui inclut maintenant la Sixième : des outils graphiques et tableaux sont introduits dans des situations particulières, des procédures variées sont dégagées et utilisées dans des problèmes. À mesure que se développe l’algèbre au cours du cycle 4, les manières d’exprimer la proportionnalité évoluent et le modèle de la fonction linéaire est explicitement étudié en Troisième. Il doit évidemment être relié aux situations de proportionnalité étudiées auparavant. Nous renvoyons au document d’accompagnement publié en 2005 [8] et toujours disponible sur Éduscol pour des repères qui nous paraissent toujours compatibles avec les programmes actuels.
Conclusion
L’expérience montre que la notion de proportionnalité n’est pas toujours bien assimilée, même par des gens très instruits, voir par exemple ![]() .
.
Cependant, c’est une notion essentielle au collège, parce qu’elle représente la première apparition de la notion de fonction et c’est peut-être la plus importante pour toutes les applications des mathématiques : on entend des ingénieurs dire que la seule notion mathématique dont ils se soient servis dans leur carrière est la règle de trois ! C’est aussi le premier point de repère du citoyen dans le foisonnement des chiffres fournis par les medias. Pour donner un exemple actuel très simple, c’est la notion pertinente pour comparer le développement de la pandémie dans les divers pays en le rapportant à leurs populations.
Pour compléter nos propos, nous renvoyons le lecteur désireux d’approfondir la question aux références qui servent d’appui à ce texte, notamment Hersant [9] et Simard [10] outre celles citées plus haut, ainsi qu’à de nombreux textes présents dans leur bibliographie et que nous n’avons pas la place de citer ici.
Références
- [1] Y. Chevallard et M. Bosch. « Les grandeurs en mathématiques au collège. Partie 1. Une Atlantide oubliée ». In : Petit \(x\) n°55 (2001) pp 5-32. ↩
- [2] Y. Chevallard et M. Bosch. « Les grandeurs en mathématiques au collège. Partie 2. Mathématisons ». In : Petit \(x\) n°59 (2002) pp 43-76. ↩
- [3] D. Perrin. Mathématiques d’école. Paris : Cassani, 2011.↩
- [4] Groupe Mots. « Grandeurs et mesures ». In : Mots. Réflexions sur quelques mots-clés à l’usage des instituteurs et des professeurs. T. Tome VI. APMEP, 1982. ISBN : 2-902680-23-6. ↩
- [5] A. Simard. « Proportionnalité en CM 2 et Sixième ». In : Petit \(x\) n°90 (2012) pp 35-52.↩
- [6] COPREM. Contributions à l’enseignement mathématiques contemporain : la proportionnalité. CNDP (CNDP Strasbourg), 1986. ↩
- [7] M.-J. Perrin-Glorian. « Réflexions dans la perspective de nouveaux programmes pour les cycles 2 (CP – CE2) et 3 ( CM1 – Sixième ) ». In Contributions aux travaux des groupes d’élaboration des projets de programmes C2, C3 et C4 (2014).
 ↩
↩ - [8] MEN Proportionnalité au collège. Document d’accompagnement des programmes 2005.
 . 2005↩
. 2005↩ - [9] M. Hersant. « La proportionnalité dans l’enseignement obligatoire en France, d’hier à aujourd’hui ». In : Repères – IREM n°59 (2005), pp5-41. ↩
- [10] A. Simard. « Fondements mathématiques de la proportionnalité dans la perspective d’un usage didactique ». In : Petit \(x\) n°89 (2012) pp 51-62.↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Daniel Perrin est géomètre-algébriste, professeur honoraire à l’université de Paris-Saclay ; tout au long de sa carrière, il a participé à la formation des professeurs, à l’ENS, à l’IUFM de Versailles, à Orsay, où il a aussi été à l’initiative de la création d’une licence pluri-disciplinaire accueillant de futurs professeurs des écoles.
Marie-Jeanne Perrin-Glorian est didacticienne des mathématiques, professeur émérite à l’université d’Artois, membre du laboratoire de didactique André Revuz (LDAR) ; elle a enseigné à l’université Paris 7 pendant vingt-sept ans où elle a participé à la création de l’IREM avant de contribuer à la formation des professeurs du primaire et du secondaire à l’IUFM Nord-Pas-de-Calais.
Ils co-animent actuellement un groupe de travail sur la géométrie au collège à l’IREM de Paris.mail_des_auteurs
- La Commission Permanente de Réflexion sur l’Enseignement des Mathématiques créée en 1983 a contribué à l’élaboration des programmes de 1985 et écrit une brochure contenant deux textes: l’un sur la proportionnalité
 et l’autre sur le calcul numérique.↩
et l’autre sur le calcul numérique.↩ - Nous reviendrons sur les grandeurs dans le paragraphe suivant. Disons seulement pour le moment qu’une grandeur est une qualité d’un objet, qu’on peut ajouter et comparer deux grandeurs de même espèce et qu’on peut multiplier une grandeur par un nombre réel positif. On peut aussi mesurer les grandeurs en les comparant à une grandeur de même espèce choisie comme unité.↩
- Il semble manquer l’additivité mais, si l’on extrapole un peu la définition de Monge et Guinchan, en remplaçant les entiers par des réels, on obtient : « On dit que deux grandeurs mesurables sont proportionnelles si, lorsqu’on multiplie (ou l’on divise) la mesure de l’une par un nombre réel \(\lambda\), la mesure correspondante de l’autre est multipliée (ou divisée) par \(\lambda\). » En appelant \(f\) l’application qui aux valeurs de l’une des grandeurs associe celles de l’autre, on a, pour tous \(x\) et \(\lambda\), \(f(\lambda x)=\lambda f(x)\) et le théorème 1(voir §3) implique que \(f\) est linéaire, donc qu’on a aussi l’additivité.↩
- Comme Platon le dit avec un brin de mépris : les calculateurs divisent, les savants multiplient.↩
- Pour calculer \(t\), ils procèdent d’ailleurs souvent en effectuant \((20\times P)\) puis en divisant par \(100\), sans même écrire \( t = \dfrac{20\times P}{100}\), ce qui ne facilite pas la suite des calculs !↩
- Bulletin officiel 30 du 26-07-2018.↩
- Pour parler de proportionnalité, on a besoin d’une addition sur les grandeurs, ce qui n’est pas le cas des grandeurs qui ne disposent que d’une relation d’ordre. Pour plus de précisions sur les grandeurs, on pourra se reporter à Chevallard et Bosch [1,2], Perrin [3] ou à la brochure Mots VI de l’APMEP [4].↩
- On peut trouver une tentative d’articulation des différentes notions dans une proposition de repères pour une progression sur les cycles 2 et 3 dans [7].↩
