Quel accès aux apprentissages géométriques
pour les élèves dyspraxiques ?
« Le trouble développemental de la coordination (TDC), ou dyspraxie, est un trouble fréquent […] se manifestant principalement dans des habiletés gestuelles, et se traduisant souvent par des difficultés d’apprentissage à l’école » [1], notamment en géométrie. Édith Petitfour nous présente un dispositif de travail qu’elle a conçu et expérimenté, visant à favoriser les apprentissages géométriques des élèves dyspraxiques en cycle 3.
Édith Petitfour
© APMEP Septembre 2022
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
À l’école primaire et en début de collège, l’enseignement de la géométrie plane s’appuie sur des manipulations et résolutions de problèmes qui nécessitent des actions instrumentées. Utiliser des instruments pour analyser une figure ou réaliser des tracés est une injonction des programmes scolaires et est supposé contribuer à l’acquisition des concepts géométriques. Cependant, cette méthode d’enseignement ne convient pas à tous les élèves, et notamment aux élèves dyspraxiques 1, empêchés d’apprendre lorsqu’ils doivent manipuler du matériel. Ces élèves n’ont pourtant pas de difficultés de compréhension qui pourraient faire obstacle au raisonnement, ils sont tout à fait en capacité d’apprendre. Ainsi que le soulignent Mazeau et Le Lostec [2] : « L’enfant dyspraxique est ainsi très souvent mis en difficulté par la méthode d’enseignement, les procédures préconisées et/ou le matériel pédagogique utilisé (et non par les connaissances ou le concept à acquérir) ».
Face à l’échec d’élèves dyspraxiques en géométrie, j’ai entrepris des recherches pour trouver un moyen d’accès à des apprentissages dans ce domaine pour ces élèves, autrement qu’en les mettant en situation de handicap avec des activités impliquant leurs habiletés gestuelles.
Dans cet article, j’illustre d’abord les difficultés que peut rencontrer un élève dyspraxique lorsqu’il est amené à réaliser une action avec du matériel, à partir d’un exemple simple, celui d’un tracé à la règle. Je présente ensuite un dispositif de travail visant à rendre accessibles les apprentissages géométriques aux élèves dyspraxiques.
Difficultés rencontrées par les élèves dyspraxiques dans une action instrumentée : tracer à la règle
Analyse préalable
Portons un instant attention à une tâche familière aux élèves très tôt dans leur scolarité : réaliser un tracé à la règle. Que doit-on faire, à quoi doit-on être attentif si l’on veut, par exemple, tracer un segment ayant pour extrémités deux points donnés ?
Notre intention d’agir [3] est pilotée par le but final poursuivi, tracer un segment, et donc relier les deux points donnés par un trait droit. On doit décider de l’instrument à prendre (la règle, pour utiliser son bord rectiligne), de son positionnement (la règle placée sur les deux points) et du tracé (d’un point à l’autre, le long de la règle).
Des actions périphériques à l’action principale de tracer sont à réaliser au préalable : se procurer une règle et un crayon (trouver ce matériel dans ses affaires ou prendre l’initiative d’en emprunter), tailler son crayon si besoin, organiser son espace de travail pour travailler sur une surface plane. Une organisation motrice et spatiale entre ensuite en jeu. On effectue des mouvements pour positionner la règle par ajustements successifs en glissant la règle tenue par les deux mains ou alors on place la mine du crayon sur un point avec la main dominante, puis on amène la règle contre la mine et on la pivote jusqu’à l’autre point avec l’autre main. On veille à ce que la règle aille de part et d’autre des deux points. On tient compte de l’épaisseur de la mine du crayon en décalant un peu la règle des points. On maintient fermement la règle avec la main non dominante, en ayant par exemple les doigts écartés sur la partie centrale de l’instrument tout en ne dépassant pas le bord le long duquel on veut tracer. Avec la main dominante, on trace une ligne continue le long de la règle en allant d’un point à l’autre. On garde une souplesse du poignet pour déplacer le crayon bien contre la règle. On appuie plus fort sur la règle que sur le crayon lorsque l’on trace pour éviter que la règle ne bouge. On contrôle sa vitesse de tracé pour pouvoir s’arrêter à temps sur le point (et ne pas non plus aller au-delà de la règle). On adopte une posture corporelle qui permette de voir le trait durant sa réalisation et donc de contrôler visuellement ses mouvements.
L’apprentissage du tracé à la règle dans un type de tâche géométrique se réalise au Cours Préparatoire. Les élèves, à force d’entraînement, automatisent les gestes à accomplir pour les réaliser ensuite sans plus y porter attention. Les élèves dyspraxiques, eux, ne sont pas en mesure d’automatiser ces gestes malgré la répétition et malgré même un entraînement intensif. La tâche de tracer à la règle, présente en géométrie mais aussi dans des tâches scolaires (souligner, relier, barrer), ne sera jamais routinière et restera, pour eux, difficile…
Un exemple avec un élève dyspraxique de CM2
Voyons par exemple ce qui se passe avec Cyril, 10 ans, élève dyspraxique de CM2 à qui j’ai demandé de tracer un segment d’extrémités deux points donnés (figure 1).
Au premier essai, Cyril maintient bien la règle. Il trace une ligne droite le long de la règle, mais il l’a positionnée un peu trop en dessous des deux points (problème de contrôle visuel). Il s’en rend compte (« Ah ! Ça va pas ! ») et souhaite recommencer le tracé. Au deuxième essai, la règle, cette fois bien positionnée au départ sur les deux points, bouge quelque peu au moment du démarrage du tracé (mauvais dosage dans la pression de stabilisation de la règle par la main non dominante) : elle ne passe plus que par un des deux points. La ligne tracée est droite, elle suit la règle. Cyril achève le tracé à main levée pour atteindre le deuxième point au moment où il s’aperçoit du problème (« J’ai bougé ! »).

Il souhaite de nouveau recommencer le tracé pour le réussir. Au troisième essai, la règle, bien positionnée, est bien maintenue. En revanche, Cyril démarre le tracé un peu après le premier point (problème de contrôle visuel) et l’achève plus loin que le deuxième en allant au-delà de la règle (problème de contrôle de la vitesse de tracé) : « Arh, j’ai dérapé ! » s’exclame-t-il. Le quatrième essai envisagé est finalement abandonné : la mine du crayon casse, recasse lors de la taille du crayon, se coince dans le taille-crayon, le taille-crayon se renverse…
Quelques caractéristiques sur les effets de la dyspraxie en appui sur l’exemple
Avant de se lancer dans la manipulation de la règle, Cyril savait très précisément comment devait être le tracé qu’il tentait de faire : son intention d’agir est intacte. À la fin de chaque essai, il repère bien ce qui ne convient pas et souhaite recommencer. Il ajuste alors son action, améliorant ce qui n’a pas fonctionné, mais il échoue pour d’autres raisons.
| L’élève dyspraxique n’est a priori pas en mesure d’obtenir de façon efficace le tracé qu’il souhaite lorsqu’il exécute une action instrumentée. Il ne parvient pas à gérer simultanément les contraintes qui mèneraient immédiatement à la production voulue, ce qui est le propre de son handicap. Le contrôle permanent et l’attention que nécessite une action avec un instrument génèrent une grande fatigue. |
Ce fait est souvent ignoré de l’entourage (l’enseignant, les autres élèves) pour qui l’action automatisée ne demande plus aucun effort. Même si l’élève dyspraxique sait qu’il doit bien maintenir sa règle, qu’il ne doit pas aller trop vite, etc., il échoue. Lui donner de tels conseils aurait peu de chances de contribuer à l’amélioration de ses tracés. S’acharner sur la transmission d’un savoir-faire pratique risquerait aussi de le détourner du réel objet d’enseignement géométrique (les connaissances relatives au concept de segment par exemple).
Il arrive parfois que l’élève dyspraxique réussisse son tracé du premier coup, mais cette performance ne devient jamais une régularité. La qualité de ses productions reste fluctuante au cours du temps, dépendante de son état de fatigue, du temps dont il dispose, etc. Cette irrégularité dans la réalisation d’une même tâche conduit parfois les enseignants non avertis à des interprétations erronées du type « Quand il veut (quand il s’applique, quand il se concentre, etc.), il peut réussir ses tracés ». Les raisons des productions imprécises et peu soignées de l’élève dyspraxique ne dépendent pas de sa « bonne volonté ». Elles sont toutes autres, non apparentes physiquement : le handicap cognitif est invisible. En plus de la lenteur, Mazeau [4] met en avant une autre conséquence pernicieuse de la dyspraxie en situation scolaire : la difficulté à gérer la double tâche.
« Si la tâche de bas niveau (telle la lecture ou le graphisme) n’est pas automatisée — ce qui est le cas du jeune dys — absorbant toute la charge mentale disponible, il ne lui restera plus assez de ressources pour la tâche seconde qui est généralement la tâche cible lors d’un apprentissage. » [4, p. 144-145]
Convaincue de la nécessité absolue d’abandonner toute manipulation d’instruments par les élèves dyspraxiques pour leur enseigner la géométrie, j’ai été amenée à concevoir et expérimenter un dispositif de travail visant à favoriser leurs apprentissages géométriques dans le cadre d’une scolarisation inclusive en classe ordinaire.
Dispositif de travail en dyade
Origine du dispositif et premières expérimentations
J’ai élaboré ce dispositif de travail en dyade2, il y a quelques années, lors d’une recherche menée sur les conditions favorables aux apprentissages géométriques des élèves dyspraxiques. Dans ce cadre, j’ai observé durant une année scolaire une élève diagnostiquée dyspraxique dans sa classe de Sixième ordinaire pendant les séances de mathématiques consacrées à la géométrie. Je cherchais à identifier ce qui pouvait faire obstacle à ses apprentissages et ce qui aurait pu constituer un levier pour lui permettre de progresser. Cette élève se retrouvait très souvent, à l’insu de sa professeure de mathématiques, en situation de handicap face à l’enseignement proposé. Elle ne pouvait en profiter pleinement, notamment lorsqu’étaient en jeu des manipulations : utilisation d’un compas, d’une équerre, de papier calque ; pliage, découpage, … Enrichie au fur et à mesure de mes observations et analyses, je menais parallèlement des séances expérimentales, en dehors des temps de classe, avec cette élève et une de ses camarades de classe. De ce travail a émergé ma proposition de dispositif de travail en dyade [5] et des pistes d’aide aux élèves dyspraxiques lorsqu’ils bénéficient en classe d’une aide humaine [6] .
J’ai par la suite mené différentes expérimentations, en collaboration avec des collègues professeurs qui accueillaient des élèves dyspraxiques dans leur classe en fin d’école primaire – début de collège, pour « faire vivre » le dispositif en classe, l’adapter aux contraintes de la classe afin qu’il produise les effets escomptés. Le dispositif devait donner un accès à des apprentissages géométriques aux élèves dyspraxiques, tout en permettant aux autres élèves de progresser dans ce domaine.
Visées et fondements du dispositif de travail en dyade
Le dispositif de travail en dyade vise à offrir des opportunités d’apprentissages géométriques à des élèves pour qui la manipulation d’instruments est un obstacle (élèves dyspraxiques entre autres). Il vise aussi à réduire, pour tout élève, le saut cognitif existant dans l’enseignement entre une géométrie organisée autour de l’action avec des instruments et une géométrie plus discursive avec l’usage du langage géométrique (formulation de programmes de construction, démonstration).
Le dispositif de travail en dyade s’ancre dans une conception vygotskienne3 de l’apprentissage comme phénomène social : la formation des concepts mathématiques se réalise à travers des interactions sociales, dans un travail conjoint autour de la résolution d’un problème. Le dispositif est basé sur un travail géométrique dans lequel les élèves collaborent dans le cadre de constructions instrumentées. Le principe consiste à remplacer les situations d’action instrumentée pour l’élève dyspraxique par des situations au plus proches de l’action, mais sans action effective, tout en produisant des effets analogues au niveau des apprentissages géométriques. Ces situations s’appuient sur des compétences préservées de l’élève dyspraxique (raisonnement, langage oral, mémoire). Ainsi, l’élève dyspraxique ne réalise aucune manipulation d’instruments et ne s’occupe pas non plus des aspects organisationnels du travail. L’élève non dyspraxique s’en charge. L’élève dyspraxique exprime son intention d’agir par des instructions langagières, accompagnées si besoin de gestes (pointage ou parcours avec l’index ou la main des objets dont on parle). Cette production gestuelle met en jeu un investissement corporel nécessitant une précision bien moindre que celle attendue pour une production graphique. L’élève non dyspraxique exécute les actions instrumentées demandées. L’élève dyspraxique éprouve alors ces actions via l’activation de ses neurones miroirs4, par observation, sans se préoccuper des caractéristiques manipulatoires de l’action. Il bénéficie aussi d’une rétroaction concordante avec ses instructions, sur laquelle peut s’appuyer sa réflexion. Le dispositif fait ainsi le sacrifice d’un développement de l’autonomie matérielle en classe de l’élève dyspraxique au profit d’une autonomie de son activité intellectuelle.
Enfin, le dispositif nécessite des compétences langagières, dont le développement est présenté dans la partie suivante.
Langage technique
Dans le cadre d’activités géométriques avec des instruments, nous introduisons le langage technique. Ce langage permet de formuler son intention d’agir autrement que par le langage géométrique, non immédiatement accessible aux élèves lors de leurs premières rencontres avec les concepts géométriques.
| Dans le domaine de la géométrie, le langage technique est relatif à l’usage des instruments en lien avec les propriétés géométriques dont ils sont porteurs. Il permet d’exprimer la mise en relation de tracés géométriques avec un instrument donné pour produire un nouveau tracé ou vérifier une propriété géométrique. |
Le langage technique s’introduit en situation, dans l’idéal au moment de la découverte d’un instrument géométrique, par ses fonctions (tracer, analyser un tracé) et ses usages. Au regard des instructions officielles actuelles [8], on introduit par exemple la règle au CP comme instrument de tracé de segments ou de vérification d’alignements, l’équerre en CE1 comme instrument de tracé d’angles droits ou de repérage de tels angles, le compas en CE1 pour tracer un cercle et en CE2 pour reporter une longueur sur une droite déjà tracée ou pour comparer des longueurs de segments.
Dans nos expérimentations dans des classes de cycle 3, nous avons procédé avec les élèves, au préalable de la mise en œuvre du dispositif de travail en dyade, à un rappel sur le rôle des différents instruments et à une mise au point sur le vocabulaire technique qui serait à employer lors des échanges au sein de la dyade.
Rôle des instruments
Nous convenons avec les élèves de nous restreindre aux rôles et usages spécifiques des instruments, même si « en vrai »5 on peut faire autrement. On peut bien sûr en pratique utiliser l’équerre pour prolonger un segment puisque cet outil a des bords droits, mais dans le langage technique, on mentionne comme instrument la règle dont c’est le rôle d’accomplir cette action. On peut tout aussi bien parfois, par souci d’économie gestuelle6, entreprendre le tracé d’un angle droit avec la règle seulement, en l’orientant par perception visuelle, mais on ne considère pas cet instrument comme approprié pour réaliser ce tracé7.
Vocabulaire technique
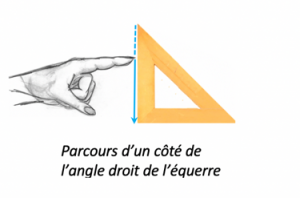
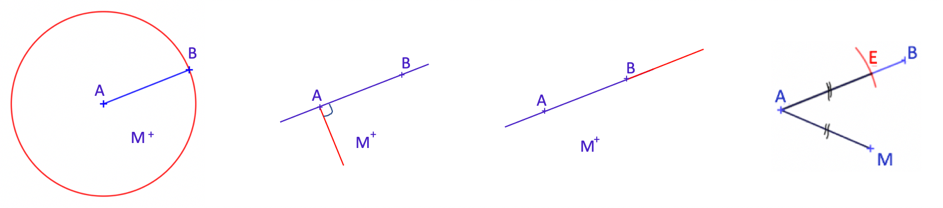
Nous associons aux termes techniques une exploration gestuelle des parties d’instruments qui sont à mettre en relation avec les tracés géométriques. On parcourt le « bord droit de la règle » avec le doigt (figure 2), bord qui serait à mettre sur un segment que l’on souhaiterait prolonger, à mettre sur deux points d’une droite que l’on voudrait tracer, ou encore à mettre sur des points dont on voudrait vérifier l’alignement, etc. On désigne avec le doigt la « pointe du compas » (figure 3), pointe que l’on associerait au centre d’un cercle que l’on voudrait tracer, on parcourt « l’écart pointe-mine du compas » (figure 4), en prenant soin d’aller en ligne droite, longueur qui correspondrait au rayon du cercle.
|
|
|
|
|---|
Le moment d’exploration de l’équerre se révèle particulièrement utile pour beaucoup d’élèves, même en Sixième, pour leur permettre de dépasser leur conception erronée de la notion d’angle droit. Lorsqu’on leur demande de montrer l’angle droit de leur équerre, ils sont nombreux en effet à désigner le sommet de cet angle ou une petite zone proche de ce sommet, peut-être en lien avec le signe graphique réalisé usuellement pour coder cet angle.
Nous les amenons alors à percevoir l’angle et ses différents constituants (côtés et sommet) : l’enseignante parcourt l’angle droit de l’équerre du tableau par un balayage avec l’avant-bras (figure 5) et les élèves celui de leur équerre par un balayage avec la main (figure 6).

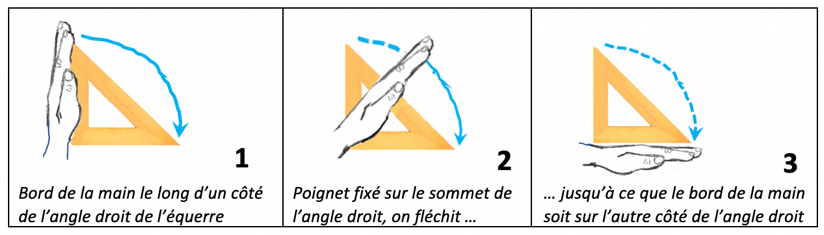
On termine par le parcours avec le doigt d’un « côté de l’angle droit de l’équerre » (figure 7), de l’autre et enfin par le pointage du « sommet de l’angle droit de l’équerre » (figure 8).
 |
 |
| Figure 7. | Figure 8. |
Règles de fonctionnement du travail en dyade
Les deux membres de la dyade ont chacun un rôle bien défini : l’un est instructeur, l’autre constructeur. Ils suivent des règles de communication spécifiques que l’on introduit lors d’un temps collectif en classe, en appui sur un échange en dyade entre l’enseignant et un élève autour d’une action instrumentée. L’enseignant prend le rôle du constructeur et guide l’élève sur ce qu’on attend de lui en tant qu’instructeur. Un autre exemple est donné ensuite avec une dyade élève-élève pour renforcer l’appropriation des interactions attendues.
Voici les règles de fonctionnement de la dyade, illustrées avec l’exemple suivant (figure 9) : il s’agit pour l’instructeur de faire réaliser un tracé (en rouge sur son document) sur l’amorce à disposition du constructeur (en bleu). Un codage (en noir) indique une relation géométrique. Le constructeur dispose d’instruments de géométrie (règle, équerre, compas).
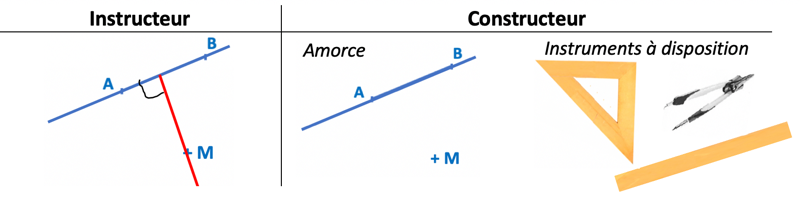
L’instructeur donne des instructions orales pour que le constructeur réalise le tracé voulu sur l’amorce. L’instructeur n’a pas le droit de manipuler les instruments. Il doit s’exprimer dans un langage technique. Les questions suivantes guident la formulation des instructions dans ce langage :
- Quel instrument utiliser ?
- Quel positionnement pour cet instrument ?
- Où tracer ?
La figure 10 présente un exemple d’interactions entre instructeur et constructeur.
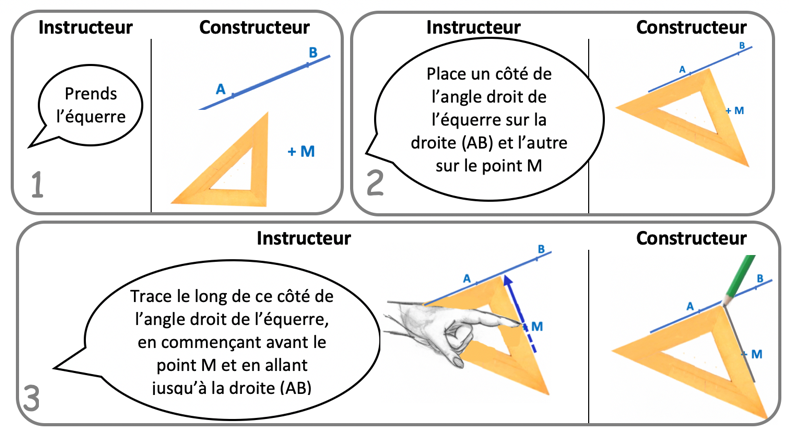
- L’instructeur mentionne l’instrument à utiliser, le constructeur s’en saisit.
- L’instructeur décrit ensuite le positionnement de l’instrument en indiquant les relations entre instrument et tracés présents, le constructeur positionne l’instrument comme demandé.
- L’instructeur donne des indications sur le lieu du tracé, complétées si besoin par des gestes montrant où la ligne doit être tracée par rapport à l’instrument, le constructeur réalise le tracé.
Notons que des gestes peuvent accompagner le langage technique (parcours ou pointage de parties d’instruments et d’objets géométriques dont on parle) mais en aucun cas le remplacer : les déictiques (« ici », « là », etc.) ou les termes spatiaux (« en haut », « à gauche », etc.) qui se substitueraient aux termes géométriques (« point », « droite », etc.) ne sont pas autorisés. Notons aussi que la façon d’amener l’instrument dans le positionnement voulu (le glisser, le tourner, etc.), ainsi que des précautions manipulatoires (« décaler un peu l’équerre de la droite (\(\mathsf{AB}\)) pour tenir compte de l’épaisseur de la mine du crayon », « bien maintenir l’équerre », etc.), ne font pas partie des instructions : le constructeur procède comme il l’entend. Comme aide-mémoire de ces règles à observer par l’instructeur, nous dressons une liste de « mots interdits » :
- Avance un peu, tourne encore, stop, recule, …
- Ici, là, par ici, là-bas, …
- En haut, tout en bas, au-dessus, à droite, …
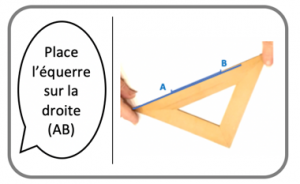
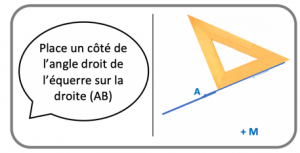
Le constructeur manipule les instruments en suivant les instructions données au fur et à mesure par l’instructeur : il prend l’instrument, le positionne et réalise le tracé comme demandé. Lors de l’étape de positionnement de l’instrument, il suit scrupuleusement les instructions, tout en essayant de ne pas répondre aux attentes de l’instructeur si elles n’ont pas été formulées explicitement. Il s’agit ainsi pour lui d’agir en « faisant le moins probable », d’éviter toute connivence avec l’instructeur, sans toutefois « faire preuve de mauvaise foi ». Le but est d’impliquer pleinement le constructeur dans la mise en jeu des connaissances géométriques lors de la construction, mais aussi de renvoyer des rétroactions immédiates sur la qualité des formulations proposées par l’instructeur, ce dernier devant tenter alors de les améliorer en levant les implicites. Revenons à l’exemple précédent (figure 9). Si l’instructeur demande de placer l’équerre sur la droite \((\mathsf{AB}\)), le constructeur peut la positionner par exemple comme sur la figure 11 : il place bien un côté de l’équerre (donc l’équerre) sur la droite (\(\mathsf{AB}\)) mais pas un côté de l’angle droit de l’équerre comme souhaité probablement par l’instructeur. Cela amène ce dernier à ajuster sa demande. S’il demande ensuite le placement d’un côté de l’angle droit de l’équerre sur la droite (\(\mathsf{AB}\)), le constructeur fera en sorte de ne pas faire passer l’autre côté de l’angle droit par le point \(\mathsf{M}\) comme attendu, puisque cela n’a pas été demandé (figure 12).
|
|
|
|---|
Pour des constructions dans l’environnement papier-crayon avec comme instruments disponibles la règle non graduée, l’équerre et le compas, cinq types d’actions instrumentées élémentaires peuvent être travaillés au départ pour s’approprier le fonctionnement du travail en dyade, ainsi que le langage technique : une de ces actions est présentée en figure 9 et les quatre autres en figure 13.
Le dispositif de travail en dyade peut alors fonctionner dans des problèmes de reproduction ou de construction de figures géométriques avec un enchaînement d’une ou plusieurs actions de ces différents types.
Pour conclure
Rappelons que mettre les élèves dyspraxiques en situation de manipuler eux-mêmes des instruments les empêche d’accéder aux connaissances géométriques visées dans les activités de construction instrumentée. La nécessité de surmonter leurs difficultés manipulatoires et organisationnelles, associée à la possibilité de prendre appui sur le langage oral comme moyen de compensation du handicap, m’ont conduite à l’élaboration d’un dispositif de travail en dyade [3,5].
Dans les expérimentations de mise en œuvre de ce dispositif en classe, s’est posée la question d’alterner les rôles d’instructeur et de constructeur. Prendre le rôle de constructeur est possible pour des actions instrumentées élémentaires isolées si l’élève dyspraxique remplace le tracé effectif au crayon par un geste de tracé (parcours avec le doigt). Le geste a en effet l’avantage d’indiquer le tracé voulu sans laisser de trace, il nécessite une précision moindre qu’un trait au crayon.
Nous avons vu aussi parfois l’intérêt d’associer un troisième élève à la dyade, avec le rôle d’observateur. Ce dernier doit veiller à ce qu’instructeur et constructeur jouent bien leur rôle et doit prendre en note les instructions formulées conduisant à la construction voulue. Cet ensemble d’instructions en langage technique constitue un programme de tracé. Il est structuré avec les mêmes arrière-plans logiques que le langage géométrique [3], il sert ainsi de support pour rédiger un programme de construction (en langage géométrique).
Les premiers résultats expérimentaux de la mise en œuvre du dispositif de travail présenté dans cet article laissent entrevoir son potentiel pour permettre des apprentissages géométriques pour tout élève. Nous avons observé des élèves dyspraxiques, tout comme leurs pairs, entrer pleinement dans un travail géométrique dans leurs interactions autour de la résolution d’un problème géométrique. Nous explorons actuellement les apports d’un travail en dyade élève instructeur – avatar constructeur dans les apprentissages géométriques avec la contribution d’un simulateur d’interactions humaines.
Références
-
INSERM — Institut National de la Santé et de la Recherche Médicale. Trouble développemental de la coordination ou dyspraxie.
Éditions EDP Sciences, 2019.
-
M. Mazeau, C. Le Lostec. L’enfant dyspraxique et les apprentissages. Coordonner les actions thérapeutiques et scolaires. Elsevier Masson, 2010.
-
É. Petitfour, T. Barrier. « D’un cadre d’analyse de l’action instrumentée en géométrie à l’élaboration d’un dispositif de travail en dyade au cycle 3 ». In : Actes de la 19e école d’été de didactique des mathématiques ARDM, (2019). Sous la dir. de S. Coppé et É Roditi, p. 329‑349.
-
M. Mazeau. « Les troubles des apprentissages en 2020 ». Contraste n° 51. (2020), p. 139‑159.
-
É. Petitfour. « Enseignement de la géométrie en fin de cycle 3. Proposition d’un dispositif de travail en dyade ». In : Petit \(x\) n° 103. (2017), p. 5‑31.
-
É. Petitfour. « Quel accompagnement en géométrie pour des élèves dyspraxiques ? ». In : Grand \(\mathbb N\) n° 101 (2018), p. 45‑70.
-
P. Laporte, M. Mazeau. Fonctions cognitives chez l’enfant. INSERM, 2013.
-
MENJ. Repères annuels de progression, Cycle 2, Mathématiques.
2019.
-
B. Offre, M.-J. Perrin-Glorian, O. Verbaere. « Usage des instruments et des propriétés géométriques en fin de CM2 » In : Petit \(x\) n°92 (2007), p. 6‑39.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Édith Petitfour est maîtresse de conférences à l’université de Rouen Normandie et fait partie du Laboratoire de Didactique André Revuz (LDAR).
![]()
-
Nous utilisons le terme « dyspraxiques » pour désigner les élèves porteurs d’un trouble développemental de la coordination, se manifestant principalement dans les habiletés gestuelles. Le lecteur pourra consulter le rapport d’expertise de l’INSERM [1] pour avoir des informations complètes sur ce trouble des apprentissages.↩︎
-
Nous utilisons ce terme de dyade pour parler de deux individus qui s’associent pour atteindre un but commun en interagissant dans un travail conjoint, chacun ayant un rôle spécifique.↩︎
-
Lev Vygotsky, pédagogue psychologue soviétique (1896-1934).↩︎
-
« Ces neurones permettent une représentation partagée de l’action, entre celui qui l’exécute et celui qui l’observe. Ils seraient donc le support, pour l’observateur de la compréhension de l’action, de sa signification, de son but : l’observateur, qui active en grande partie les mêmes neurones que l’acteur, éprouverait ainsi lui-même l’action de l’autre. » [7, p. 54].↩︎
-
J’emprunte cette expression parlante pour les élèves à Claire Lommé, professeure de mathématiques de collège avec qui j’ai pu mettre à l’épreuve le dispositif durant trois années pour le rendre opérationnel en classe.↩︎
-
« L’économie gestuelle s’entend comme la limitation des gestes à accomplir pour un tracé ou la vérification de propriétés. » [9, p. 9].↩︎
-
Avec un logiciel de géométrie dynamique, le tracé ne résisterait pas au déplacement.↩︎

Une réflexion sur « Quel accès aux apprentissages géométriques pour les élèves dyspraxiques ? »
Les commentaires sont fermés.