Le rapporteur Recto-Verso
La double graduation des rapporteurs du commerce pose bien souvent des difficultés à nos collégiens… Notre collègue Patrice Pellegrin présente le rapporteur Recto-Verso qu’il a confectionné, permettant de ne plus se tromper entre, par exemple, un angle de 88° et un de 92° !
Patrice Pellegrin
© APMEP Mars 2023
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Pour mesurer ou pour construire un angle, l’immense majorité des élèves utilise un rapporteur dont la double graduation est souvent source d’erreurs. En effet, par exemple, lors de la lecture d’un angle avec ce type de rapporteur, quelle graduation prendre en compte ? Voyons cela sur un exemple d’angle à mesurer : faut-il lire ici 88° ou 92° ?

Rapporteur double gradution du commerce
Mon rapporteur Recto-Verso, une solution ?
Comme son nom l’indique, mon rapporteur Recto- Verso est un rapporteur gradué de 0° à 180° au recto et au verso, avec seulement un rayon tracé (à faire coïncider avec l’un des côtés de l’angle à mesurer ou à tracer) !
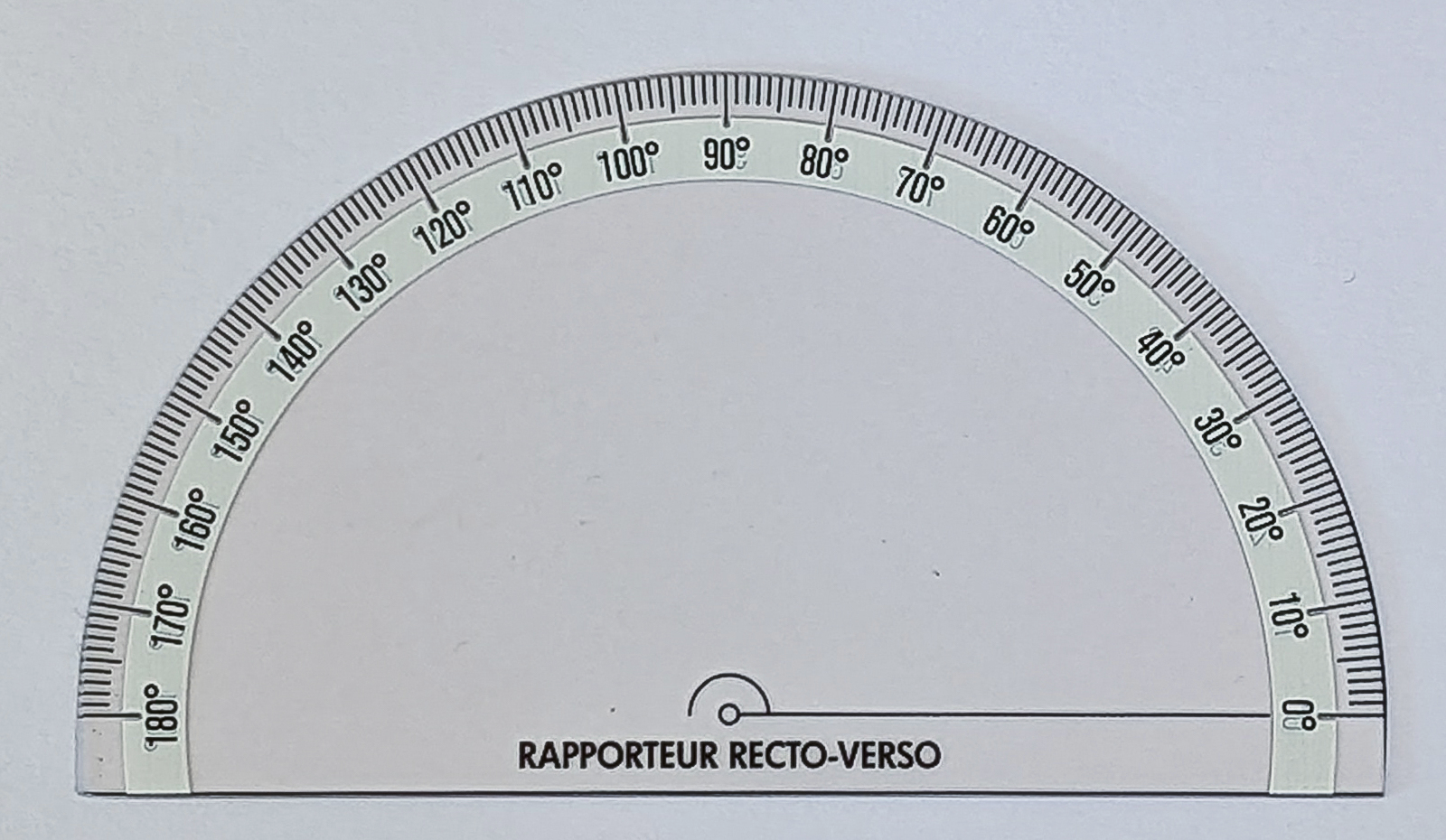 Recto du rapporteur Recto-Verso. Recto du rapporteur Recto-Verso. |  Verso du rapporteur Recto-Verso. Verso du rapporteur Recto-Verso. |
Il n’y a donc plus qu’une valeur possible lors de la lecture et donc aucun choix à faire entre deux valeurs : cela le rend ainsi beaucoup plus simple d’utilisation pour les élèves ! Utilisons-le pour mesurer l’angle précédent :
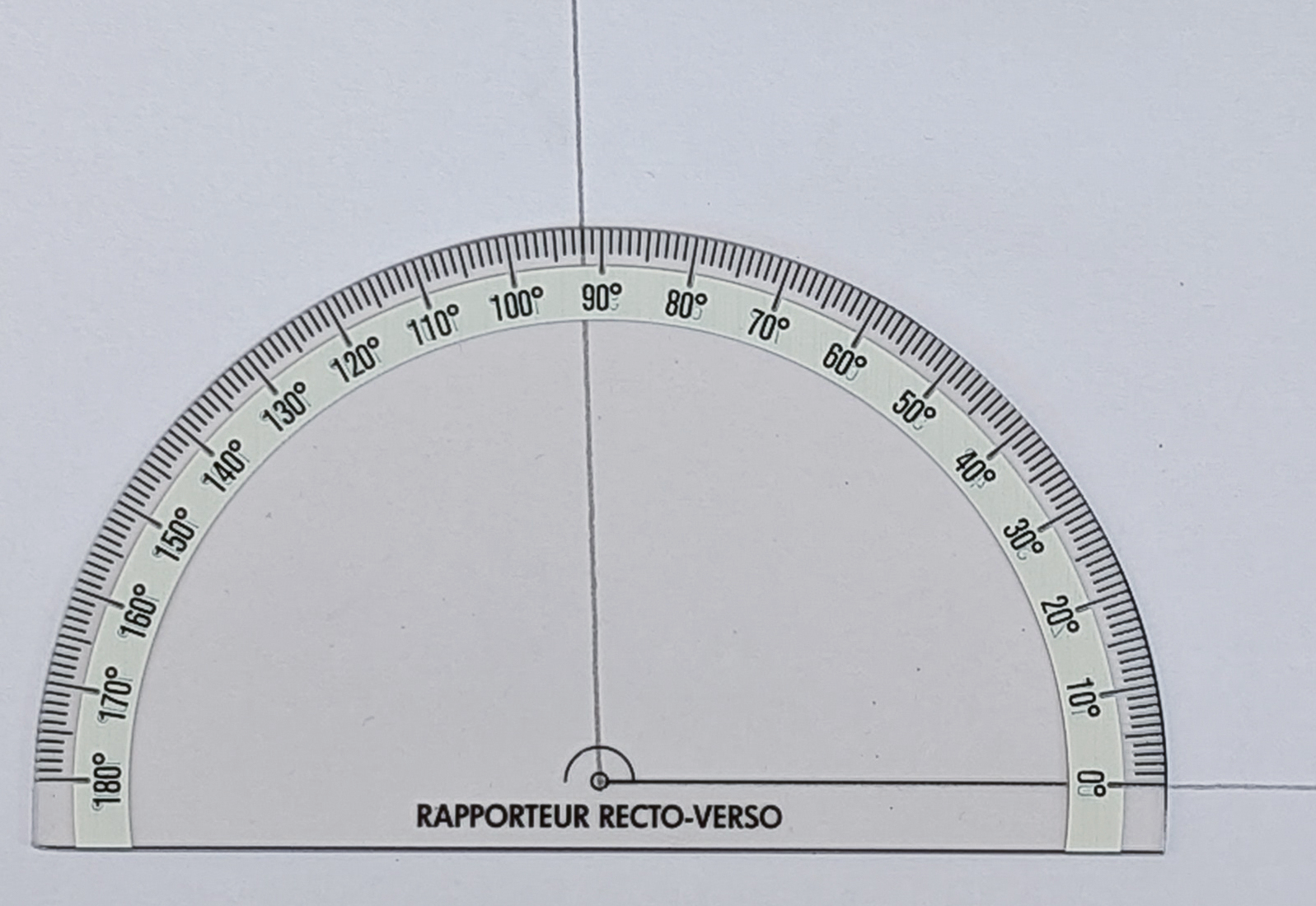 Mesurer un angle avec le recto du rapporteur. Mesurer un angle avec le recto du rapporteur. |
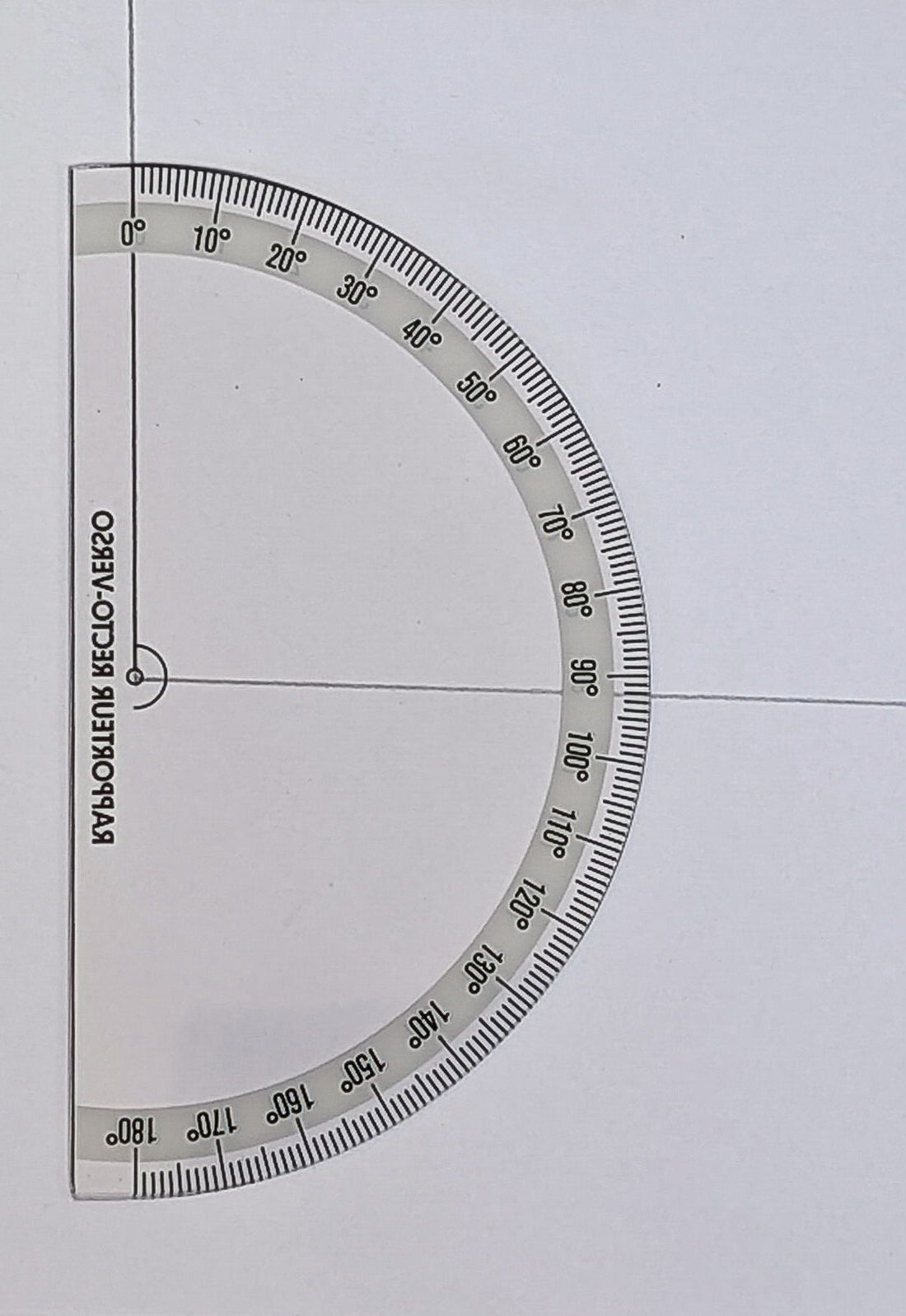 Mesurer un angle avec le verso du rapporteur. Mesurer un angle avec le verso du rapporteur. |
Pas de doute possible : la mesure de cet angle est bien 92° ! Remarquons qu’un rapporteur simple graduation aurait suffi ici, pas besoin qu’il soit Recto-Verso pour mesurer un angle (ou encore tracer un angle de mesure donnée).
En revanche pour construire un triangle connaissant une mesure et deux angles, le rapporteur Recto-Verso prend tout son intérêt. Voyons cela sur l’exemple suivant :
| Construisons un triangle \(\mathsf{ABC}\) tel que : \(\mathsf{AB} = 8\) cm, \(\widehat{\mathsf{BAC}}\) = 50° et \(\widehat{\mathsf{ABC}}\) = 40° |
Après avoir tracé le segment \([\mathsf{AB}]\) de 8 cm, on construit l’angle \(\widehat{\mathsf{BAC}}\) = 40° avec le recto du rapporteur. On termine ensuite le triangle avec l’angle \(\widehat{\mathsf{ABC}}\) de 50° avec le recto du rapporteur. On termine ensuite le triangle avec l’angle \(\widehat{\mathsf{ABC}}\) de 40° en utilisant le verso du rapporteur cette fois :
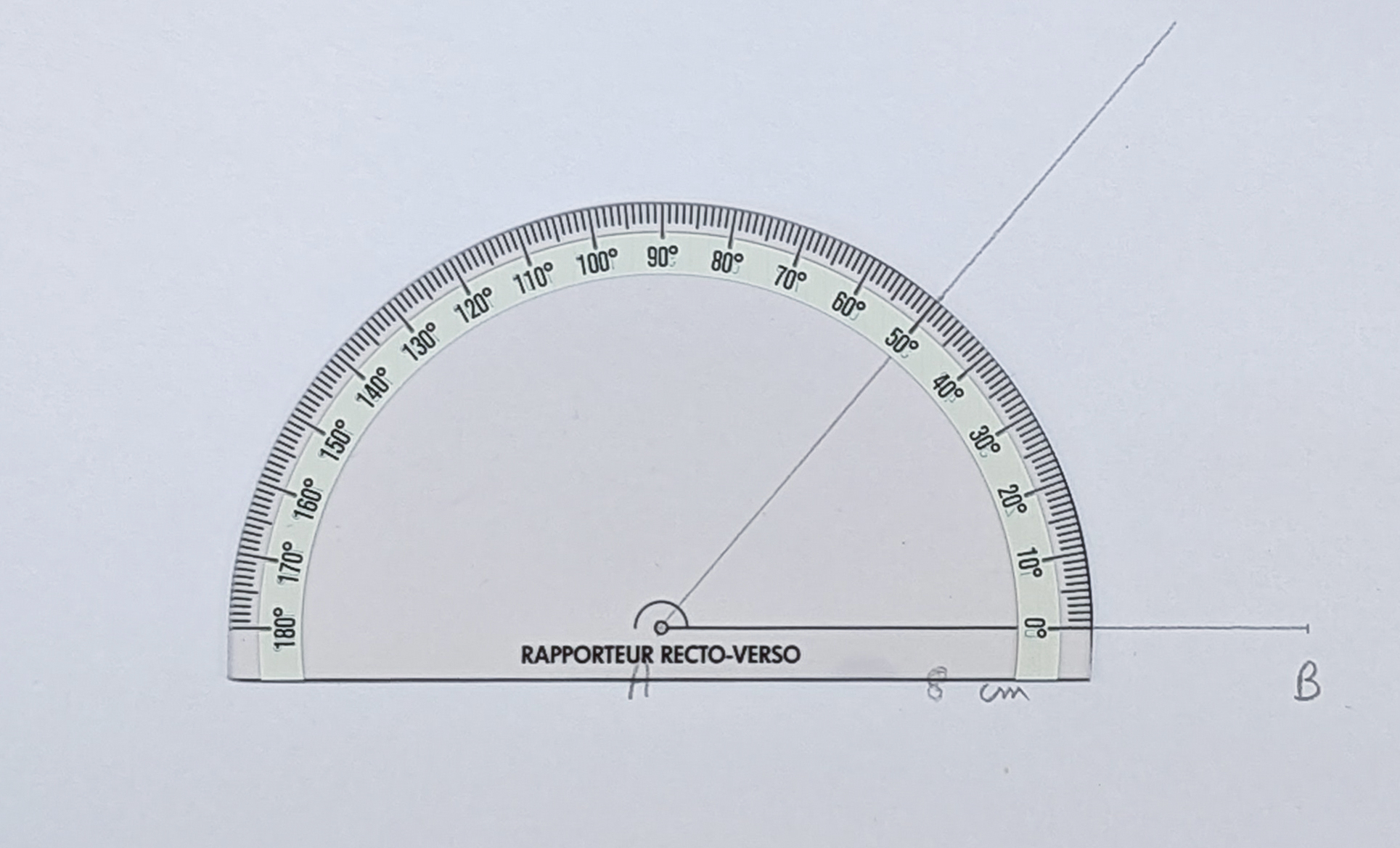 Construction du triangle, étape 1. Construction du triangle, étape 1. |  Construction du triangle, étape 2. Construction du triangle, étape 2. |
Si vous n’êtes pas convaincus, n’hésitez pas à visionner les vidéos sur mon site.

NDLR : si vous ne les connaissez pas déjà, nous vous invitons aussi à découvrir les rapporteurs circulaires de chez Aleph et Math en Main
, sociétés régulièrement présentes lors de nos Journées Nationales.
Par ailleurs, nous vous conseillons la (re-)lecture de l’article de Nicole Toussaint « Le rapporteur muet ou la transparence n’est pas si rétro… », paru dans PLOT 47 (APMEP 2014)
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Patrice Pellegrin est professeur de mathématiques dans l’académie d’Aix-Marseille.
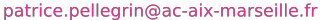

Une réflexion sur « Le rapporteur Recto-Verso »
Les commentaires sont fermés.